24歳で独学により1級ファイナンシャル・プランニング技能士を取得。2021年に「ほんださん / 東大式FPチャンネル」を開設し、32万人以上の登録者を獲得。
2023年に株式会社スクエアワークスを設立し、代表取締役としてサブスク型オンラインFP講座「FPキャンプ」を開始。FPキャンプはFP業界で高い評価を受け、2025年9月のFP1級試験では48%を超える受験生が利用。金融教育の普及に注力し、社会保険労務士や宅地建物取引士など多数の資格試験に合格している。
FP2級の金融資産運用設計において、多くの受験生が苦手意識を持つのが「計算問題」です。
特に「期待収益とリスク」の分野は、言葉の定義を正確に理解していないと、数字の意味が分からず迷子になってしまいがちです。
しかし、この分野は出題パターンが決まっているため、仕組みさえ理解すれば確実に得点源にできる「ボーナスステージ」とも言えます。
この記事では、期待収益率の計算方法から、分散投資の効果、そしてシャープレシオの使い方まで、合格に必要な知識を網羅的に解説します。
数式が苦手な方でも、イメージを膨らませながら読み進めてみてください。

金融の計算問題って聞いただけで難しそうで、公式を覚えられるか不安です。特に「リスク」という言葉が、普段使っている意味と違う気がして混乱してしまいます。



大丈夫ですよ!FP試験における「リスク」は、単なる「損」ではなく「値動きの幅」だと捉えるのがコツです。まずは基礎的な用語の定義から、1つずつ丁寧に紐解いていきましょう。一緒に期待収益とリスクをマスターして、FP2級の合格を勝ち取りましょうね!


FP試験頻出の「期待収益率」と「リスク」の定義と性質

金融資産運用の世界では、私たちが日常生活で使っている「リターン」や「リスク」という言葉とは少し異なる意味を持っています。
試験で得点するためには、まずこの定義を正確に押さえる必要があります。
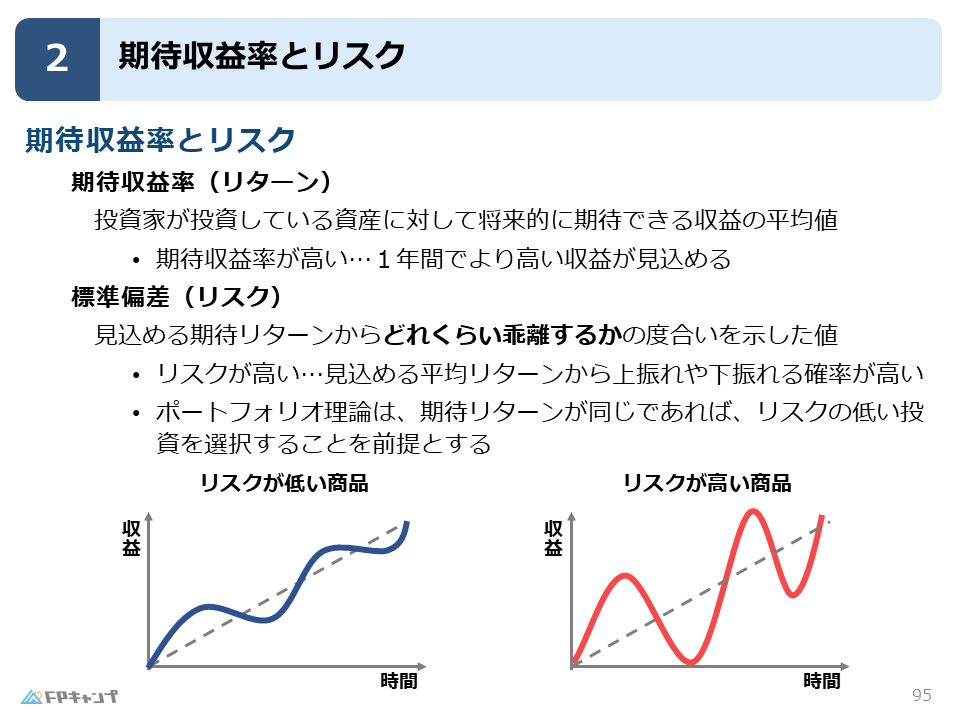
「期待収益率(リターン)」とは、投資している資産に対して将来的に期待できる収益の平均値のことです。
例えば、過去5年間や10年間の運用実績を振り返り、「平均すると1年でこれくらい儲かってきたから、来年もこれくらいは期待できるだろう」と予測する数値です
。あくまで平均値を指している点がポイントと言えるでしょう。
一方で「リスク」は、一般的には「損をする可能性」と思われがちですが、投資理論では「標準偏差」という言葉で表されます。
これは、先ほどの期待収益率(平均値)から、実際の収益がどれくらい上や下にズレる可能性があるかという「振れ幅(ボラティリティ)」を意味します。
値動きが激しい商品は、平均から大きく外れる可能性が高いため「リスクが高い」と表現されるのです。
ポートフォリオ理論においては、「同じ期待収益率であれば、よりリスク(振れ幅)が低い商品を選択する」という前提があります。
1年で5%の利益が期待できる商品が2つあった場合、値動きが穏やかな方を選ぶのが投資の基本姿勢となります。



なるほど、リスクは「損」ではなく「平均からのズレ」のことなんですね。値動きが激しい商品は、それだけ予測が難しいからリスクが高いと言われるわけですか。



その通りです!「リスクが高い=値動きが激しい」と変換して覚えるのがコツですよ。この感覚があれば、後の分散投資の理論もスムーズに理解できるはずです。
ポートフォリオ全体の期待収益率を算出する3ステップの計算手順


複数の資産を組み合わせて保有することを「ポートフォリオ」と呼びます。
FP2級の試験では、このポートフォリオ全体の期待収益率を求める計算問題が頻繁に出題されます。
計算には「加重平均」という手法を使いますが、以下の3ステップを守れば誰でも正解を導き出せます。
1. 各資産の構成比(%)を小数にする(例:60%→0.6)
2. 各資産ごとに「構成比(小数)×期待収益率(%)」を計算する
3. 全資産の計算結果を合計する
それでは、具体的な例題で計算してみましょう。
預金、債券、株式を以下の割合で保有しているポートフォリオを想定します。
| 資産の種類 | 保有比率(構成比) | 期待収益率 | 計算式(構成比×収益率) |
|---|---|---|---|
| 預金 | 60%(0.6) | 0.1% | 0.6 × 0.1 = 0.06% |
| 債券 | 15%(0.15) | 1.0% | 0.15 × 1.0 = 0.15% |
| 株式 | 25%(0.25) | 8.0% | 0.25 × 8.0 = 2.0% |
| 合計 | 100% | – | 2.21% |
このように、各資産の期待収益率に「重み(比率)」を掛けて足し合わせるのが加重平均の特徴です。
単純に収益率を足して資産数で割る「単純平均」とは結果が異なりますので、必ず構成比を掛けることを忘れないでください。



計算自体は掛け算と足し算だけなので、手順さえ間違えなければ得点できそうです!構成比を小数にするのを忘れないように気をつけます。



素晴らしいですね!この計算は期待収益とリスクの問題の中でも特に得点しやすい部分です。ケアレスミスを防ぐために、電卓を叩く前に一度構成比の合計が100%(1.0)になっているか確認する癖をつけましょう。
分散投資によるリスク低減効果と「加重平均」の引っかけ対策


期待収益率の計算では「加重平均」を使いましたが、ポートフォリオのリスク(標準偏差)については注意が必要です。
ポートフォリオ全体のリスクは、各資産のリスクを単純に加重平均した値よりも小さくなるという性質があります。
これは、異なる動きをする資産を組み合わせることで、お互いの値動きを打ち消し合う効果(分散効果)が働くためです。
試験では「ポートフォリオのリスクは、各資産のリスクの加重平均と等しくなる」といった誤った選択肢が出ることがあります。
正解は「加重平均した値よりも低減される」ですので、しっかりと区別しておきましょう。
また、リスクには「消せるリスク」と「消せないリスク」の2種類が存在します。
銘柄数を増やすことで減らすことができるリスクを「アンシステマティックリスク(非体系的リスク)」と呼びます。
特定の企業の不祥事や業績悪化などによるリスクは、他の銘柄を持つことでカバーできる可能性があります。
一方で、どれだけ分散投資をしても消すことができないリスクが「システマティックリスク(体系的リスク)」です。
これは市場全体の変動、例えばリーマンショックや世界的な不況など、すべての資産に影響を与える要因から生じるリスクを指します。



「システマティック」は市場全体のシステムだから消せない、と覚えればいいんですね。アンシステマティック(非システマティック)はその逆だから、分散で消せると考えれば分かりやすいです。



その通り!カタカナ用語は混乱しやすいので、イメージで捉えるのが合格への近道です。リスクは分散で小さくなりますが、ゼロにはならないという点も覚えておいてくださいね。
相関係数による分散効果の違い:1から-1までの数値の意味


分散投資の効果がどれくらい発揮されるかは、資産同士の「値動きの似通い具合」によって決まります。
これを示す指標が「相関係数」です。
相関係数はプラス1からマイナス1までの値を取り、その数値によって分散効果の大きさが変わります。
| 相関係数の値 | 値動きの関係性 | 分散投資の効果 |
|---|---|---|
| +1 | 全く同じ動きをする | 効果なし(リスクは減らない) |
| 0 | 全く関係なく動く | 効果あり |
| -1 | 完全に逆の動きをする | 効果は最大(リスクを最小にできる) |
相関係数が「1」の場合、2つの資産は双子のように全く同じ動きをします。
一方が下がればもう一方も同じだけ下がるため、組み合わせて持ってもリスクを抑えることはできません。
逆に「-1」の場合は、一方が下がればもう一方が必ず上がるという関係になるため、理論上はリスクをゼロに近づけることが可能になります。
FP2級の試験でよく狙われるのが「相関係数が0」のときです。
0は「全く関係がない」状態ですが、分散効果はしっかりと存在します。
「0だから効果がない」という引っかけ問題には注意が必要です。
少しでも1より小さければ、何らかの分散効果が得られると理解しておきましょう。



マイナス1のときに分散効果が最大になるんですね。プラス1だと、同じ船に乗っているようなものだから意味がない、というイメージでしょうか。



分かりやすい例えですね!理想はマイナスに近い組み合わせを探すことですが、現実的には相関係数がプラスであっても、1より小さければリスク低減の効果は期待できると言われています。
投資の効率性を測る「シャープレシオ」の計算式と判定方法

投資信託などの運用成績を比較する際、単に「どれくらい儲かったか(収益率)」だけを見るのは不十分です。
大きなリスクを取って高い収益を得たのか、小さなリスクで効率よく収益を得たのかを判断する必要があります。
そのための指標が「シャープレシオ」です。
シャープレシオの計算式は以下の通りです。
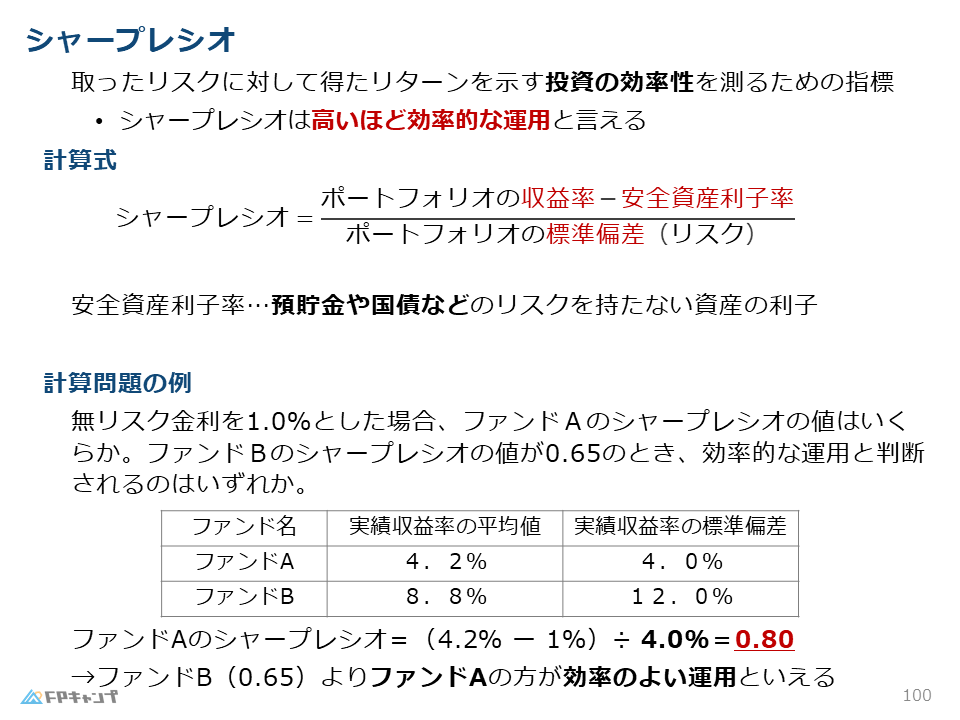
シャープレシオ =(ポートフォリオの収益率 - 安全資産利子率)÷ 標準偏差(リスク)
ここで「安全資産利子率(無リスク金利)」とは、預金や国債のように、リスクを全く取らなくても得られる利益のことです。
収益率からこの安全資産利子率を引くことで、リスクを取ったことによって得られた「上乗せ分の利益(超過収益)」を算出します。
その上乗せ分をリスク(標準偏差)で割ることで、1単位あたりのリスクでどれだけ効率的に稼げたかを数値化するのです。
シャープレシオの数値が高いほど、リスクに対して効率的な運用がなされていると判断されます。
例えば、以下の2つのファンドを比較してみましょう(安全資産利子率を1.0%と仮定します)。
・ファンドA:収益率4.2%、標準偏差4.0%
シャープレシオ = (4.2 - 1.0) ÷ 4.0 = 0.80
・ファンドB:収益率5.2%、標準偏差6.0%
シャープレシオ = (5.2 - 1.0) ÷ 6.0 = 0.70
収益率だけを見ればファンドBの方が魅力的に見えますが、リスクとのバランスを考えた効率性では、シャープレシオが高いファンドAの方が優れていると言えます。



シャープレシオの計算式、一見複雑そうですけど「リスク1あたりのご褒美」を求めていると考えれば覚えやすいですね。分母がリスク、分子が頑張って稼いだ上乗せ利益!



その解釈、素晴らしいです!シャープレシオは計算問題としても、用語の正誤問題としても非常に出やすいので、必ずマスターしておきたいポイントと言えるでしょう。
【まとめ】期待収益とリスク FP2級 合格 を確実にする計算問題の重要ポイント
ここまで「期待収益とリスク」について解説してきましたが、いかがでしたでしょうか。
最後に、試験直前に見直したい重要ポイントを整理します。
1. 期待収益率は各資産の「加重平均」で求める。
2. ポートフォリオのリスクは、加重平均した値よりも「小さくなる」性質がある。
3. 銘柄を増やしても消せないリスクは「システマティックリスク」。
4. 相関係数が「-1」のとき、分散効果は最大になる。
5. シャープレシオは「(収益率-安全資産利子率)÷標準偏差」で求め、数値が高いほど効率が良い。
これらのポイントは、FP2級の金融分野で非常に高い頻度で出題されます。
最初は難しく感じるかもしれませんが、一度計算の手順に慣れてしまえば、確実に点数を積み上げられる武器になります。
テキストの例題や過去問を繰り返し解いて、数字に慣れておきましょう。
期待収益とリスクの概念を正しく理解することは、試験対策だけでなく、自分自身の資産運用を考える上でも非常に役立つ知識です。
一歩ずつ着実に学習を進めて、合格を目指して頑張りましょう!



計算のステップと、リスクの性質が整理できて自信がつきました!特に相関係数やシャープレシオの考え方は、暗記ではなく意味で捉えられたので忘れない気がします。



その調子です!金融科目は用語の壁さえ乗り越えれば、得点源にしやすい科目です。もし迷ったら、またこの記事を読み返して基本に立ち返ってくださいね。応援しています!