係数の計算問題（ライフプランニングと資金計画）完全講義シリーズ

「6つの係数を丸暗記しないと解けない…」と不安になっていませんか？

本記事では、FP2級の頻出テーマである「6つの係数」を、公式や名前を覚えずとも解けるようになるためのポイントを解説します。

最後まで読むことで、複利計算のロジックが理解でき、係数を使った問題にスムーズに取り組めるようになります。

係数とは？資産運用と複利計算の関係を理解する

係数とは、将来の資産額や必要な積立額などを簡単に計算するためのツールです。

資産運用においては、利息に利息がつく複利でお金が増えていきますが、年数が長くなるほど計算は複雑になります。

そこで、係数を使えば手軽に結果を導けるわけです。

複雑な計算をシンプルに：なぜ係数を使うのか

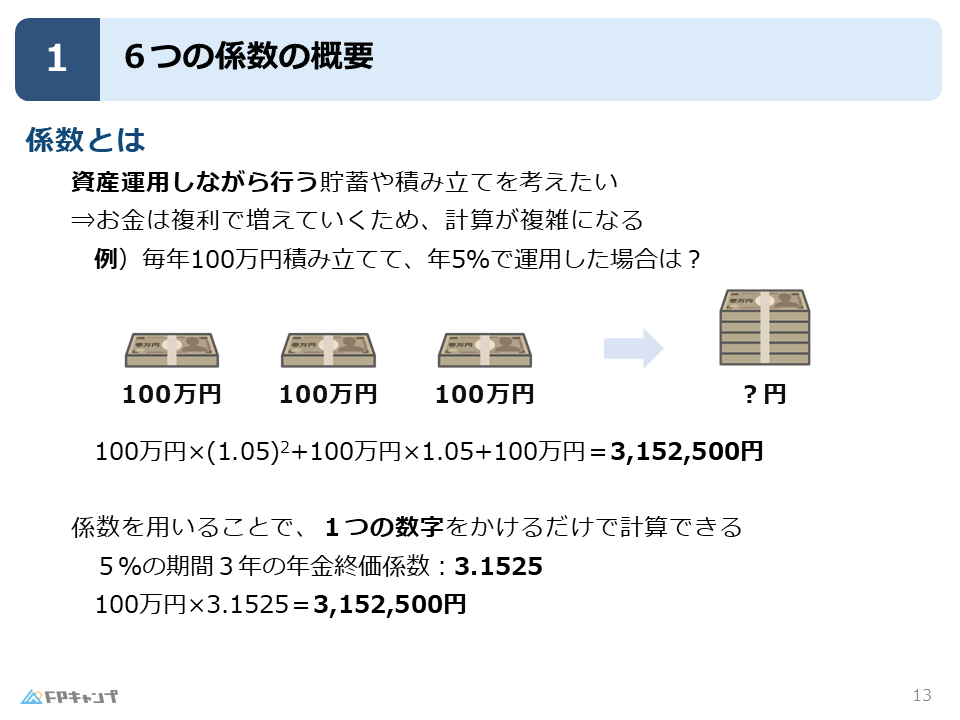
複利計算を手作業で行うと、1年目 → 2年目 → 3年目…と累積で算出しなければならず非常に手間です。

例えば、毎年100万円を年利5%で3年間積み立てた場合、通常は複数ステップの計算が必要ですが、「年金終価係数」をかけるだけで一気に最終金額を求められます。

具体的な計算例：年間100万円の積立で将来いくらになる？

3年間、毎年100万円を複利年5%で積み立てて運用する場合、3年後の積立額は、100万円×3.1525=315万2500円となります。

この3.1525という数字が、5%、3年間の年金終価係数です。

係数を使うことで、複雑な複利計算をしなくても、簡単に将来の積立額を求めることができます。

FP2級に出題される6つの係数とは？

6つの係数一覧：それぞれの役割を把握する

係数名	説明	何を求めるか
終価係数	現在の一時金を将来どれくらいになるか計算する係数	将来価値
現価係数	将来のある金額を現在価値に換算するための係数	現在価値
年金終価係数	一定期間、毎年積み立てたお金の将来価値を計算する係数	将来価値
減債基金係数	将来のある金額を目標に、毎年いくら積み立てれば良いか計算する係数	毎年の積立額
資本回収係数	現在のある金額を一定期間で取り崩していく場合、毎年いくら取り崩せるか計算する係数	毎年の取り崩し額
年金現価係数	将来、毎年受け取れるお金の現在価値を計算する係数	現在価値

上記のように、6つの係数はそれぞれ異なる役割を持っています。名前の暗記よりも、「どんなシチュエーションで使うか」を理解することが鍵です。

図解で理解：3つの運用パターン

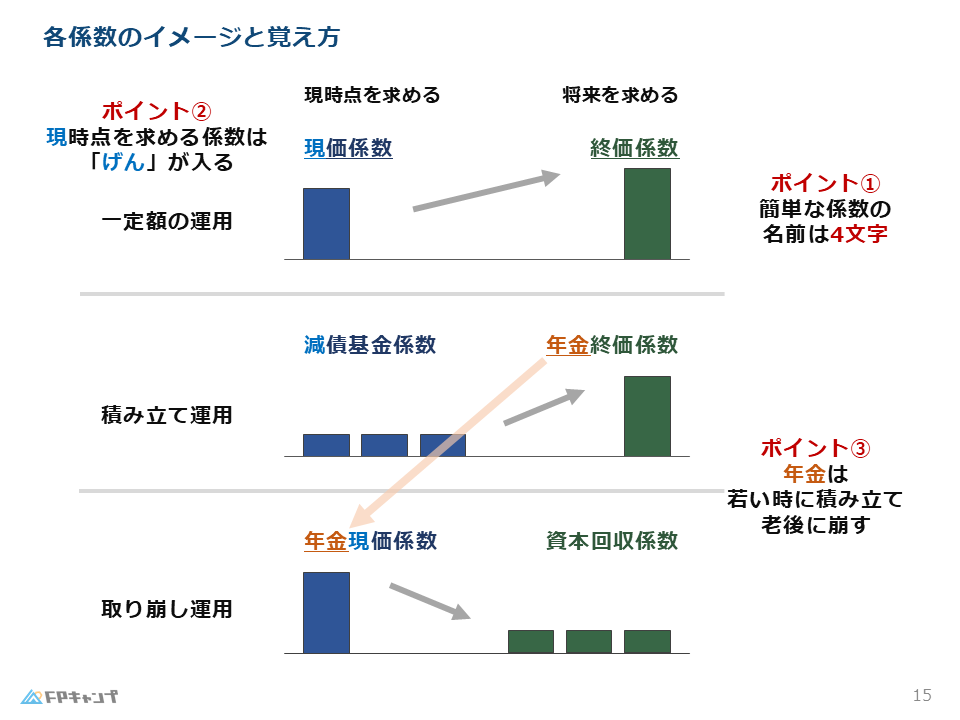
一定額運用：終価係数

現在ある一定額のお金を運用した場合、将来どれくらいの金額になるかを求めるには、終価係数を使います。

例えば、現在100万円を年利5%で10年間運用した場合、将来の資産額は100万円 × (終価係数) で計算できます。

この場合、複利で計算するため、単純に利息を足していくよりも大きな金額になります。

積立運用：年金終価係数など

毎年一定額を積み立てて運用した場合、将来どれくらいの金額になるかを求めるには、年金終価係数を使います。

例えば、毎年100万円を年利5%で10年間積み立てて運用した場合、将来の積立額は100万円 × (年金終価係数) で計算できます。

こちらも複利で計算されるため、積立額以上の金額になります。

取り崩し運用：資本回収係数など

現在ある一定額のお金を一定期間で取り崩していく場合、毎年どれくらいの金額を取り崩せるかを求めるには、資本回収係数を使います。

例えば、現在1000万円を年利5%で10年間で取り崩していく場合、毎年取り崩せる金額は1000万円 × (資本回収係数) で計算できます。

複利で計算されるため、単純に1000万円を10で割った額より多く取り崩せます。

高頻度出題問題の解き方：学科試験・実技試験の例題

学科試験と実技試験の例題

学科試験では、「年率2%で複利運用しながら、10年後に100万円を得るためには毎年いくら積み立てれば良いか」といった問題が出題されます。

ここでは「減債基金係数」を使用します。実際には係数表で2%、10年の値を探し、
必要な積立額 = 100万円 × 減債基金係数
で計算します。

実技試験では、「一定額を積み立てて年3%で複利運用し、20年後に1500万円となるためには、毎年いくら積み立てれば良いか」といった問題が出題されます。

こちらも同じく減債基金係数を使い、
1500万円 × 係数 = 毎年の積立額
となります。

FP2級 係数の計算：解法ステップをマスター！

ステップ1：複利を無視した係数の値を予想する

まずは、問題文で問われている内容を理解し、複利を無視した場合、係数の値がどれくらいになるかを予想します。

例えば、10年間毎年100万円を受け取るために必要な元本を求める問題では、複利を無視すると100万円 × 10年 = 1000万円となります。

この10という数字が、複利を無視した場合の係数の値の目安になります。

ステップ2：予想値と実際の係数の大小関係を判定する

複利を考慮すると、実際の係数が予想値より大きくなるか小さくなるかを判定します。

現在価値を求める場合は、予想値よりも小さく。

将来価値を求める場合は、予想値よりも大きく。

これを把握すると、係数表で適切な数字をすばやく見つけやすくなります。

ステップ3：係数表から適切な値を選択する

最後に、ステップ1とステップ2を踏まえて係数表から該当する数値を選び、計算します。
問題文で与えられた「金利」と「期間」、そして「何を求めるか」に応じて係数を選ぶだけです。

係数表はFP試験で必ず提供されるので、見方をしっかり理解しておきましょう。

これができれば、係数の計算も効率的に行えるようになります。

FP2級 係数の計算：実践演習！ 学科試験の過去問に挑戦

問題文から必要な情報を抽出する

例題：「10年間に渡り、年率2%で複利運用しながら毎年100万円を受け取るために必要な元本はいくらか。」

将来毎年100万円を受け取る目標があり、そのための現在の元本を求める問題。つまり現在価値を求めます。

金利は2%、期間は10年。このように、問題文を丁寧に読むことで必要な情報を抽出します。

解法ステップに沿って解答を導く

ステップ1：複利を無視すると、100万円×10年=1000万円。

ステップ2：現在価値なので、予想値より小さくなる。

ステップ3：2%、10年に対応する年金現価係数を係数表で探す（例：8.9826）。

結果、100万円×8.9826=898万2600円が必要な元本となります。

FP2級 係数の計算：暗記ではなく理解！ FP試験攻略の鍵

効率的な学習方法：考える力を養う

FP試験では、知識の丸暗記だけでなく、本質的な理解が求められます。

係数の計算も同様で、ただ公式を覚えるより、「なぜその式になるのか」「何を求めているのか」を意識して勉強しましょう。

問題文のどこに着目すればいいのかを掴んでおけば、係数表を見ただけで正しい計算が導けます。

資産運用の実践的な知識にもつながるので、一石二鳥です。

まとめ：暗記より理解！ FP試験攻略の鍵

• 6つの係数は、それぞれ「どのタイミングの金額」を求めるかで使い分ける
• 係数名を全部覚えるより、「将来価値か、現在価値か」を明確に把握する方が効果的
• 係数表の見方をマスターすれば、複利計算をシンプルに処理できる

いかがでしたか？ 「なぜこの係数が必要なのか」を理解するほど、問題がスムーズに解けるようになります。

ぜひ今回紹介したポイントを押さえて、過去問や演習問題に挑戦してみてください。FP2級合格への大きな一歩を踏み出せるはずです。